Schritt 2: Normalkraft \(N_\xi\) als Funktion des Schnittwinkels \(\varphi\) bestimmen
Tüfteln wir gemeinsam! Bereit für die nächste Herausforderung? In diesem Schritt entlarven wir die geheime Identität der Normalkraft \(N_\xi\) – mithilfe des Kosinus!
Zuerst werfen wir einen genauen Blick auf das Kräftedreieck an einer beliebigen Schnittfläche in Abbildung 1.2.10. Siehst du das? Da versteckt sich ein trigonometrischer Zusammenhang zwischen dem Schnittwinkel \(\varphi\), der Normalkraft in \(\xi\)-Richtung \(N_\xi\) und der Normalkraft in x-Richtung \(N_x\).

Stellt dir vor, \(N_\xi\) ist eine schüchterne Person, die sich hinter \(N_x\) versteckt. Aber mit dem Kosinus-Trick können wir sie entlarven!
- Winkel \(\varphi\) und Hypotenuse \(N_x\) sind bekannt.
- Gesucht: die Ankathete \(N_\xi\).
Ein bisschen Umformulieren und schon haben wir:
(3)
Aha! Die Normalkraft \(N_\xi\) ist proportional zur x-Komponente \(N_x\) und dem Kosinus des Schnittwinkels \(\varphi\). Je größer der Winkel, desto mehr traut sich \(N_\xi\) aus der Deckung hervor. Und: Da \(\cos(\varphi)\) mit steigenden \(\varphi\) abnimmt, nimmt auch \(N_\xi\) ab.
- Formel (3) ist dein magischer Schlüssel, um die Normalkraft \(N_\xi\) zu berechnen.
- Winkel \(\varphi\) und \(N_x\) sind die Zutaten für den Zaubertrank.
- Mit dem Kosinus-Trick entlarvst du die geheime Identität der Normalkraft!
P.S.: Falls du noch mehr Magie brauchst, schau dir die trigonometrischen Beziehungen genauer an.
P.P.S.: Vergiss nicht, dass \(N_\xi\) positiv oder negativ sein kann. Je nachdem, welche Richtung die Kraft hat.
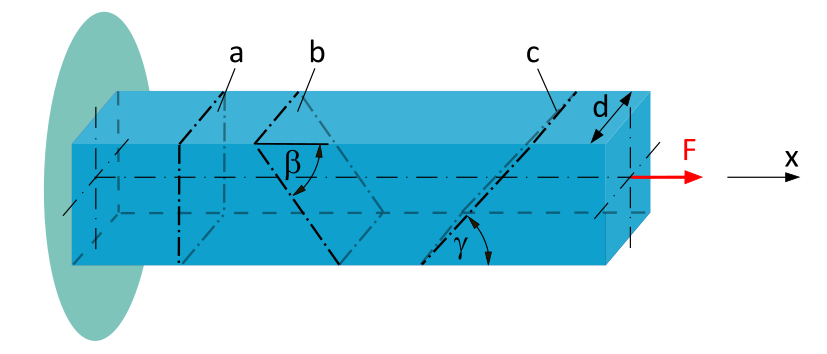
Normal- und Schubspannung unter beliebigem Schnittwinkel
Ein eingespannter Balken mit quadratischem Querschnitt (Seitenlänge \(d=20~\mathrm{mm}\)) wird durch eine Zugkraft \(F=10~\mathrm{kN}\) in der Balkenachse belastet.
Bestimme die mittlere Normalspannung und die mittlere Schubspannung, die
- in der Schnittebene a wirken.
- in der Schnittebene b (\(\beta = 50°\)) wirken.
- in der Schnittebene c (\(\gamma = 40°\)) wirken.