Funktionsgleichungen aufstellen

Lineare Funktionen aufstellen

Lineare Funktionen beschreiben Geraden. Die Aufgabe besteht für uns also darin, aus einer in einer Grafik gegebenen Geraden die beschreibende Geradengleichung aufzustellen.

Wie sieht diese Geradengleichung im Allgemeinen aus? Lineare Funktionen haben die folgende Form:

$$ \begin{aligned} y = m \cdot x + b\qquad \end{aligned} $$

m: Steigung
b: Schnittpunkt mit der y-Achse

$x$ und $y$ sind die Punkte auf der gesuchten Geraden, d.h. für jedes $x$, das wir in die Gleichung einsetzen, bekommen wir am Ende den dazugehörigen $y$-Wert dieser Geraden. Was wir also bestimmen müssen, sind die Werte m (Steigung der Geraden) und b (Schnittpunkt der Geraden mit der y-Achse).

In typischen Aufgabenstellungen der Technischen Mechanik haben wir es mit einem der folgenden Fälle zu tun. Sie unterscheiden sich dadurch, dass unterschiedliche Werte gegeben sind:

Fall 1: Ein Punkt der Funktion, sowie der Schnittpunkt mit der y-Achse sind gegeben:

Oft haben wir den Fall, dass in einem Aufgabentext oder einer grafischen Darstellung der gesuchten linearen Funktion der Schnittpunkt der Funktion mit der y-Achse sowie beispielsweise der Nullpunkt der Funktion gegeben ist.

Beispiel für einen Aufgabentext: Zum Zeitpunkt t=0 wirkt ein Drehmoment von 1000 Nm, welches innerhalb von 10 s linear auf 0 Nm abfällt.

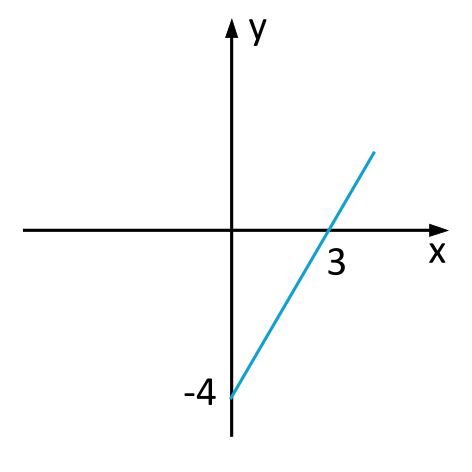
Die folgende Grafik zeigt eine weitere Beispielfunktion mit gegebenem Punkt sowie Schnittpunkt mit der y-Achse:

Die Grafik zeigt eine Funktion mit gegebenem Punkt P(3;0) und den Schnittpunkt mit der y-Achse (-4; 0). — Abb. 1: Lineare Beispielfunktion mit gegebenem Punkt sowie Schnittpunkt mit der y-Achse

Rezept, um die gesuchte lineare Funktion aufzustellen:

Schnittpunkt $b$ direkt ablesen. In der obigen Grafik liegt der Schnittpunkt der Funktion mit der y-Achse bei $b=-4$
Die Gleichung der linearen Funktion (s.o.) nach $m$ umstellen,

$$ \begin{aligned} y = m \cdot x + b\qquad \Rightarrow \qquad m=\dfrac{y-b}{x} \end{aligned} $$

den bekannten Punkt $(x|y) = (3|0)$ und $b=-4$ einsetzen und damit $m$ berechnen:

$$ m=\dfrac{y-b}{x} = \dfrac{0-(-4)}{3}=\dfrac{4}{3} $$
Damit lautet die gesuchte lineare Funktion der Beispielgrafik in Abb. 1:

$$ \underline{\underline{y=f(x)=\frac{4}{3}x-4}} $$

Fall 2: Zwei Punkte der Funktion sind gegeben:

Oft haben wir auch den Fall, dass in einem Aufgabentext oder einer grafischen Darstellung der gesuchten linearen Funktion zwei Punkte, von denen keiner der Schnittpunkt mit der y-Achse ist, gegeben sind.

Beispiel für einen Aufgabentext: Zum Zeitpunkt t=2 s wirkt ein Drehmoment von 1000 Nm, welches innerhalb von 10 s linear auf 500 Nm abfällt.

Die folgende Grafik zeigt eine weitere Beispielfunktion mit zwei gegebenem Punkten:

Die Grafik zeigt eine Funktion mit den gegebenen Punkten P1(-7; 10) und P2(11; -7). — Abb. 2: Lineare Beispielfunktion mit zwei gegebenen Punkten

Rezept, um die gesuchte lineare Funktion aufzustellen:

Punkte ablesen. Dabei ist es egal, welcher Punkt $P_1(x_1|y_1)$ und welcher Punkt $P_2(x_2|y_2)$ genannt wird. Wir können also aus dem obigen Beispiel entweder ablesen:

$x_1 = -7$, $y_1=10$, $x_2=11$, $y_2 = -7$,

richtig wäre für dieses Lösungsrezept aber auch:

$x_1 =11$, $y_1=-7$, $x_2=-7$, $y_2 = 10$.
Die Formel zur Berechnung der Steigung $m$ lautet:

$$ \begin{aligned} m = \dfrac{y_2-y_1}{x_2-x_1} \end{aligned} $$

Eingesetzt nach obiger Grafik:

$$ m=\dfrac{(-7)-10}{11-(-7)}=\dfrac{-17}{18}=-\dfrac{17}{18} $$

Vertauschen wir die Punkte $P_1$ und $P_2$, erhalten wir wie oben beschrieben dasselbe Ergebnis:

$$ m=\dfrac{10-(-7)}{(-7)-11}=\dfrac{17}{-18}=-\dfrac{17}{18} $$
Die Gleichung der linearen Funktion (s.o.) nach $b$ umstellen,

$$ \begin{aligned} y = m \cdot x + b\qquad \Rightarrow \qquad b=y-mx \end{aligned} $$

einen der beiden bekannten Punkte $P_1(x_1|y_1)$ oder $P_2(x_2|y_2)$ sowie die berechnete Steigung $m$ einsetzen und damit $b$ berechnen:

$$ b=y-mx = 10 - (-\dfrac{17}{18}) \cdot (-7) = \dfrac{180-119}{18} = \dfrac{61}{18} $$
Damit lautet die gesuchte lineare Funktion der Beispielgrafik:

$$ \underline{\underline{y=f(x)=-\frac{17}{18}x + \frac{61}{18}}} $$

Quadratische Funktionen (Parabeln) aufstellen

Quadratische Funktionen beschreiben Parabeln. Die Aufgabe besteht für uns in der Technischen Mechanik also darin, aus einer in einer Grafik gegebenen Parabel die beschreibende Parabelgleichung aufzustellen.

Wie sieht diese Parabelgleichung im Allgemeinen aus? Quadratische Funktionen haben die folgende Hauptform:

$$ \begin{aligned} y = ax^2+bx+c\qquad \end{aligned} $$

$a$: Öffnungsparameter, $a\neq0$
$a$,$b$,$c$: konstante Faktoren

$a>0$: Nach oben geöffnete Parabel
$a<0$: Nach unten geöffnete Parabel

$x$ und $y$ sind die Punkte auf der gesuchten Parabel, d.h. für jedes $x$, das wir in die Gleichung einsetzen, bekommen wir am Ende den dazugehörigen $y$-Wert dieser Parabel. Was wir also bestimmen müssen, sind die Werte $a$, $b$ und $c$.

Um direkt aus der allgemeinen Form der Parabelgleichung die Funktion bestimmen zu können, benötigt man zwei Punkte $P_1$ und $P_2$ dieser Funktion sowie den Öffnungsparameter $a$. Damit können 2 Gleichungen aufgestellt werden und $b$ sowie $c$ bestimmt werden. Eine solche Aufgabenstellung kommt jedoch in der Technischen Mechanik eigentlich nie vor.

In typischen Aufgabenstellungen der Technischen Mechanik haben wir vielmehr den Scheitelpunkt $S$ der Parabel sowie einen weiteren Punkt gegeben:

Die Grafik zeigt eine Parabelfunktion mit dem Scheitelpunkt S(0; 36) und dem ebenfalls gegebenen Punkt P(10; 0). — Abb. 3: Quadratische Beispielfunktion mit gegebenem Scheitelpunkt und weiterem gegebenen Punkt

Der Scheitelpunkt $S$ ist, abhängig vom Öffnungsparameter $a$, das Minimum (nach oben geöffnet) bzw. Maximum (nach unten geöffnet) der Parabel.

Haben wir den Scheitelpunkt und einen zusätzlichen Punkt der Parabel gegeben, ist es zweckmäßig, statt der allgemeinen Form der quadratischen Funktion die Scheitelpunktform zu verwenden. Hier kann der Scheitelpunkt direkt eingesetzt werden:

$$ \begin{aligned} y = a(x-x_S)^2+y_S\qquad \end{aligned} $$

$a$: Öffnungsparameter, $a\neq0$
$x_S$, $y_S$: Koordinaten des Scheitelpunktes $S$

$a>0$: Nach oben geöffnete Parabel
$a<0$: Nach unten geöffnete Parabel

Rezept, um die gesuchte quadratische Funktion mithilfe der Scheitelpunktform aufzustellen

Scheitelpunkt $S(x_S|y_S)$ in die Scheitelpunktform einsetzen.

Beispiel mit $S(x_S|y_S)=(0|36)$ aus der obigen Grafik (Abb. 3):

$$ \begin{aligned} y=a(x-x_S)^2+y_S = a(x-0)^2+36=ax^2+36 \end{aligned} $$
Öffnungsparameter $a$ bestimmen. Dafür die unter 1. gefundene Gleichung nach $a$ umstellen und den gegebenen Punkt einsetzen. Beispiel mit $P(x|y)=(10|0)$ aus der obigen Grafik (Abb. 3):

$$ y = ax^2+36 \quad \Rightarrow \quad a=\dfrac{y-36}{x^2}=\dfrac{0-36}{10^2}= -\dfrac{36}{100}=-0,36 $$
Damit lautet die gesuchte quadratische Funktion:

$$ \underline{\underline{y=f(x)=-0,36x^2+36}} $$

Auf dieser Seite