Practice Exercise in Mathematics for Engineers

Problem M-D-1.6

Differential Calculus: Difference Quotients and Commmon Tangents of 2 Functions

Problem Statement

Given are the functions

f : x \mapsto f (x) = x^{2} + 1, D_{f} = R

and

g : x \mapsto g (x) = - x^{2} - 1, D_{g} = R

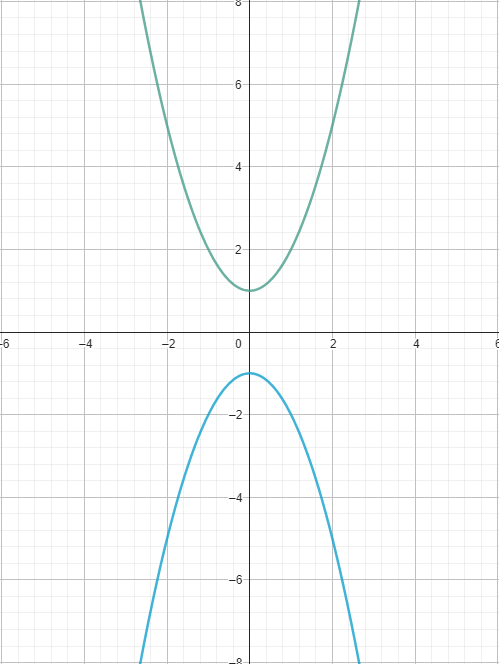
Exercise — Fig. 1: Graph $f (x) = x^{2} + 1$ and Graph $g (x) = - x^{2} - 1$

Determine the derivatives $f^{'}$ and $g^{'}$ as the limit of the difference quotient.
Provide the common tangents of $f (x)$ and $g (x)$ .

Short Solution

a. Determine the derivatives

f^{'}

and

g^{'}

as the limit of the difference quotient.

\begin{aligned} f^{'} (x_{0}) & = 2 x_{0} \\ g^{'} (x_{0}) & = - 2 x_{0} \end{aligned}

b. Provide the common tangents of

f (x)

and

g (x)

.

\begin{aligned} t_{1} (x) & = 2 x \\ t_{2} (x) & = - 2 x \end{aligned}

Comprehensive Solution

a. Determine the derivatives $f^{'}$ and $g^{'}$ as the limit of the difference quotient.

If we need to determine the derivative of a function as the limit of the difference quotient, we require the formula for the derivative of $f$ at the point $x_{0}$ (also known as the differential quotient of $f$ at the point $x_{0}$ ):

\begin{aligned} (1) & f^{'} (x_{0}) & = lim_{h \to 0} \frac{f (x_{0} + h) - f (x_{0})}{h} \end{aligned}

For all $x_{0} \in R$ and all $h \neq 0$ , the following holds:

Continue with TechMechAcademy+

Everything. Always. Everywhere.

With TechMechAcademy+ full access to all content.

Become a TechMechAcademy+ Premium Member!

Are you already a TechMechAcademy+ premium member? Then please log in here to enjoy full access to all content.

Exercise M-D-1.6